原文:
Triplanar Mapping
Summary
在前面我们介绍过二维平面映射的实现方法,这里我们来讲讲三维平面的映射方法。
纳尼?平面本身是二维的叫二维平面还可以理解,你这来个三维平面,是欺负我读书少,想糊弄我???
稍安勿躁!首先专业名字本身依据其专业用途、含义来取的,很容易和我们习惯相冲突,比如数学领域各种眼花缭乱的术语。这里我们的三维平面更多的值得是三维空间上的平面,可以有三个维度的取值。之前提到的二维平面映射,是只从一个方向进行投影,换句话说,我们只用沿着其投影方向进行渲染,才能看到我们的纹理贴合在模型表面,如果换个角度,你可能就看不到了,即便看到了也可能是模糊不清的。而三维平面映射,是从分别从三个维度进行投影映射,然后将得到的三个纹理颜色进行混合,这样无论我们采用怎样刁钻的角度,也挑不出啥毛病。
当然,本文也是在之前的二维平面映射的基础上扩展的,在了解其原理后,你也可以使用表面着色器重写一遍。

Calcualte Projection Planes
首先,为了得到三个不同方向的UV坐标,我们需要改变UV坐标的生成方式。在二维平面映射中,我们是在顶点着色器中进行UV变换。这里我们直接将顶点的世界坐标传递到片段着色器中,然后在片段着色器中进行uv变换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| struct v2f{
float4 position : SV_POSITION;
float3 worldPos : TEXCOORD0;
};
v2f vert(appdata v){
v2f o;
o.position = UnityObjectToClipPos(v.vertex);
float4 worldPos = mul(unity_ObjectToWorld, v.vertex);
o.worldPos = worldPos.xyz;
return o;
}
|
接下来我们对三个方向投影所对应的uv坐标进行UV变换。在这里我把世界坐标的y轴对应uv坐标的v,这样渲染出来的纹理就是正的。当然,你也可以随意尝试多种对应关系,看看会有什么不一样的效果。
1
2
3
4
5
6
| fixed4 frag(v2f i) : SV_TARGET{
float2 uv_front = TRANSFORM_TEX(i.worldPos.xy, _MainTex);
float2 uv_side = TRANSFORM_TEX(i.worldPos.zy, _MainTex);
float2 uv_top = TRANSFORM_TEX(i.worldPos.xz, _MainTex);
}
|
然后使用变换后的uv值进行纹理采样,并将三个不同的采样值进行平均。当然你也可以直接求和,不过最终结果会显得非常亮。
1
2
3
4
5
6
7
8
9
10
11
|
fixed4 col_front = tex2D(_MainTex, uv_front);
fixed4 col_side = tex2D(_MainTex, uv_side);
fixed4 col_top = tex2D(_MainTex, uv_top);
fixed4 col = (col_front + col_side + col_top) / 3;
col *= _Color;
return col;
|

Normals
到目前为止,你会发现整个材质表现的非常怪异,各种重影迭起,这是因为我们只是单纯的对三个方向的采样值进行平均。为了消除这种重影,我们可以根据不同的朝向,侧重显示对应朝向的采样值。表面朝向有个专业点的名称:法向向量。在我们的网格数据中就包含法向数据。因为一些特殊考虑,网格数据中的法向和顶点是一一对应的。
所以,我们首先要做的是在我们的输入结构体中加入法向变量,然后在顶点着色其中将其变换到世界坐标系,并且通过插值数据传入到片段着色器中参与后续的计算。这里之所以要变换到世界坐标系,是因为我们的纹理映射是基于世界坐标系的。换句话说,我们在进行计算时,应该保证空间数据的空间一致性。
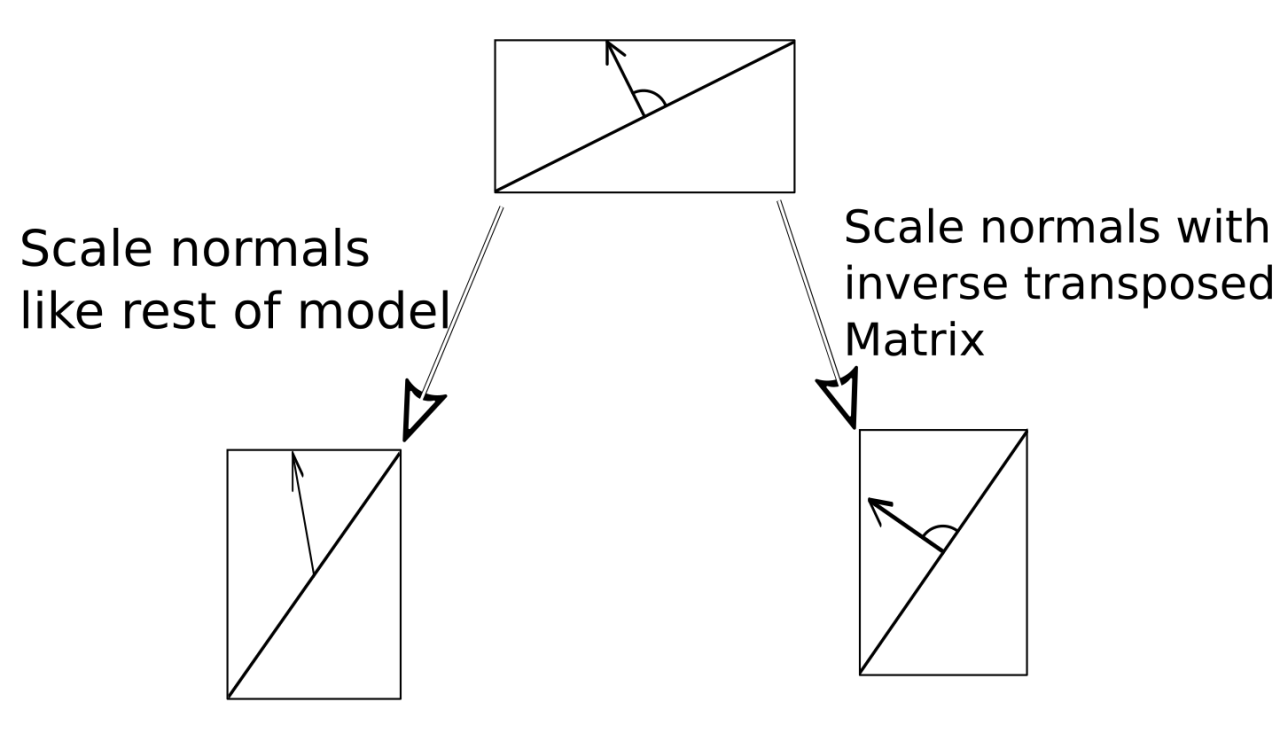
其中将法向从模型坐标系变换到世界坐标系有些特殊。一般的顶点在两个坐标系之间转换是直接乘以模型矩阵,但是法向是乘以模型矩阵转置的逆矩阵。当然其中的矩阵推导比较复杂,我们记住这个结论就行。如果你好奇心很强,那我这里可以先定性地给你分析一下为什么不能直接乘以模型矩阵。前面说过,法向是垂直与表面的向量,假设我们将模型沿着x轴正方向拉伸,这时候表面相对于y轴会变得越来越陡,如果我们也对法向做同样的拉伸,你会发现法向也变得越来越陡,这时候法向和表面不再是垂直关系。我们这里描述的拉伸实际上就是一个空间变换的操作,因此法向和顶点不能使用同样的空间变换,否则将会打破两者的垂直关系。而模型矩阵转置的逆矩阵正是一种相反的操作,可以始终保持两者的垂直关系。当然我们还需要将该矩阵裁剪为3X3的矩阵,因为4x4矩阵还包含了平移变换,而我们的法向量最为方向是没有位置的概念的,所以需要剔除掉矩阵中的平移部分。
事实上,在实际的代码中,我们可能并不会直接使用模型矩阵转置的逆矩阵,而是会采用一些小巧的方法,尽可能的减少计算量。例如世界到模型的变换矩阵刚好等于模型矩阵的逆矩阵,同时向量与矩阵乘积的顺序调转,刚好可以替代转置操作。所以实际上我们可以用法向量左乘世界到模型的变换矩阵来计算在世界坐标系下的法向量。是不是很绕、很晕?那没办法,给你一张图自己去捂捂!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| struct appdata{
float4 vertex : POSITION;
float3 normal : NORMAL;
};
struct v2f{
float4 position : SV_POSITION;
float3 worldPos : TEXCOORD0;
float3 normal : NORMAL;
};
v2f vert(appdata v){
v2f o;
o.position = UnityObjectToClipPos(v.vertex);
float4 worldPos = mul(unity_ObjectToWorld, v.vertex);
o.worldPos = worldPos.xyz;
float3 worldNormal = mul(v.normal, (float3x3)unity_WorldToObject);
o.normal = normalize(worldNormal);
return o;
}
|
在学习渲染的过程中,记住可视化是我们的看家本领,所以很多时候都可以通过渲染后的表现效果来分析我们的计算过程。这里可以将法向量进行可视化,很简单就是直接将法向量当成颜色返回。所谓的高大上的可视化到咱这还不算一行代码的事,实在不行就多写两行!
1
2
3
| fixed4 frag(v2f i) : SV_TARGET{
return fixed4(i.normal.xyz, 1);
}
|

在得到世界空间下的法向后,我们还需要对法向取绝对值才能应用到后面的权重分配部分。因为法向作为方向向量其取值是在[-1,1]之间,这也是为什么前面的法向可视化中,朝着负轴向的表面颜色是黑色。
1
2
| float3 weights = i.normal;
weights = abs(weights);
|
法向的各个轴向值得大小表明了法向与各个轴向的重合程度。所以我们将权重的各个轴向值分别乘以前面三个投影方向的采样值,例如xy投影平面的投影方向是z轴,所以将其采样值乘以z轴的权重值,依次类推。
这里我们不需要做平均,因为我们并不是简单的将三个采样值进行相加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
float3 weights = i.normal;
weights = abs(weights);
col_front *= weights.z;
col_side *= weights.x;
col_top *= weights.y;
fixed4 col = col_front + col_side + col_top;
col *= _Color;
return col;
|

上图可以看到整个模型看你来更加凝实了,少了很多眼花缭乱的重影。但是还有一个问题,前面的例子中有一个求平均的过程,但是为甚么要求平均呢,因为求平均可以保证最终混合结果不会过亮。但是我们这里使用法向权重值之和会大概率会大于1,最终导致显示过亮。所以我么可以先除以权重和。
1
2
|
weights = weights / (weights.x + weights.y + weights.z);
|

现在看起来和纹理原本的亮度差不多。
最后一步是尽可能的提高各个投影方向纹理的权重差异。因为上图的显示效果还是有很大一部分相互叠加。这是因为即便某个投影方向有权重优势,但这种优势并不是碾压式的,不能占有绝对比重。为了使强者越强、弱者越弱,指数函数是一个很好地选择。我们先定义一个表示指数的参数。然后在权重之前,对其各个分量执行指数操作。然后在材质面板上调节这个指数参数,观察显示变化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
_Sharpness("Blend Sharpness", Range(1, 64)) = 1
float _Sharpness;
weights = pow(weights, _sharpness)
|
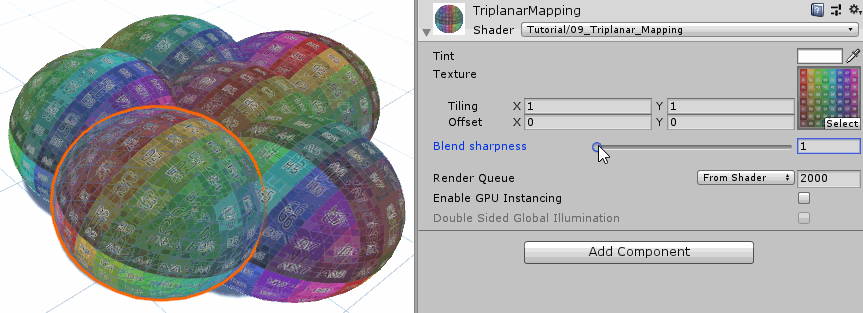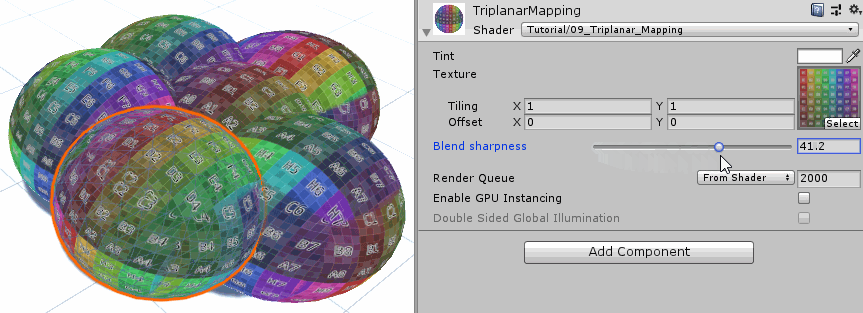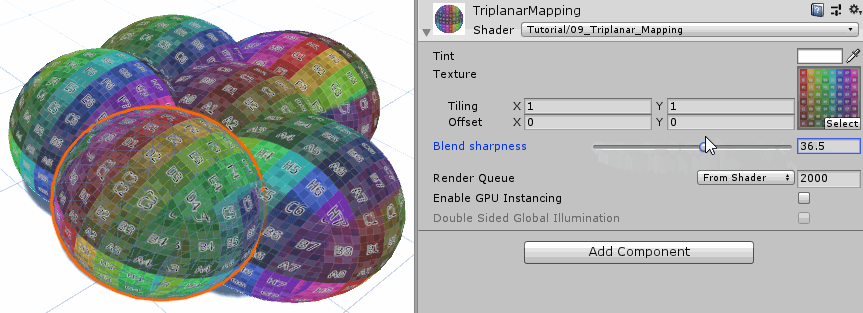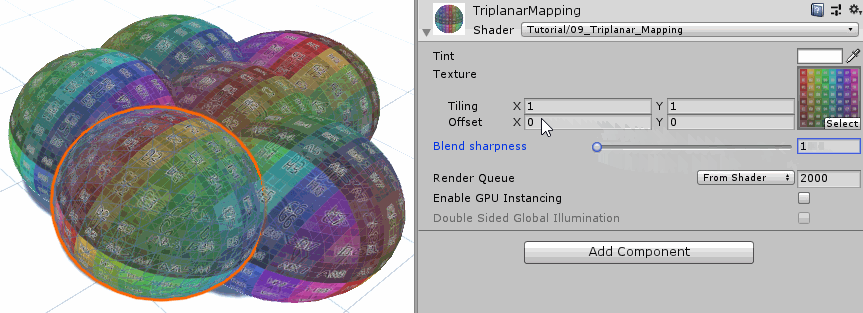
上面的三维平面映射效果还有些问题,表面45度的地方存在明显的过渡痕迹,不过这种痕迹的出现是由于纹理上下左右边界不衔接导致的。另外三维平面映射的性能消耗要更大,因为这里执行了三次纹理采样。
我们可以将三维平面映射应用在表面着色器上,例如对albedo进行三维平面映射,或者对specular等纹理。但是法向纹理需要额外的操作才行,因为我们在三维平面映射的过程中使用的法向向量,这里不做深入研究了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
| Shader "Tutorial/010_Triplanar_Mapping"{
Properties{
_Color ("Tint", Color) = (0, 0, 0, 1)
_MainTex ("Texture", 2D) = "white" {}
_Sharpness ("Blend sharpness", Range(1, 64)) = 1
}
SubShader{
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
Pass{
CGPROGRAM
#include "UnityCG.cginc"
#pragma vertex vert
#pragma fragment frag
sampler2D _MainTex;
float4 _MainTex_ST;
fixed4 _Color;
float _Sharpness;
struct appdata{
float4 vertex : POSITION;
float3 normal : NORMAL;
};
struct v2f{
float4 position : SV_POSITION;
float3 worldPos : TEXCOORD0;
float3 normal : NORMAL;
};
v2f vert(appdata v){
v2f o;
o.position = UnityObjectToClipPos(v.vertex);
float4 worldPos = mul(unity_ObjectToWorld, v.vertex);
o.worldPos = worldPos.xyz;
float3 worldNormal = mul(v.normal, (float3x3)unity_WorldToObject);
o.normal = normalize(worldNormal);
return o;
}
fixed4 frag(v2f i) : SV_TARGET{
float2 uv_front = TRANSFORM_TEX(i.worldPos.xy, _MainTex);
float2 uv_side = TRANSFORM_TEX(i.worldPos.zy, _MainTex);
float2 uv_top = TRANSFORM_TEX(i.worldPos.xz, _MainTex);
fixed4 col_front = tex2D(_MainTex, uv_front);
fixed4 col_side = tex2D(_MainTex, uv_side);
fixed4 col_top = tex2D(_MainTex, uv_top);
float3 weights = i.normal;
weights = abs(weights);
weights = pow(weights, _Sharpness);
weights = weights / (weights.x + weights.y + weights.z);
col_front *= weights.z;
col_side *= weights.x;
col_top *= weights.y;
fixed4 col = col_front + col_side + col_top;
col *= _Color;
return col;
}
ENDCG
}
}
FallBack "Standard"
}
|
希望本文能够帮助你理解什么是三维平面映射。
你可以在以下链接找到源码:https://github.com/ronja-tutorials/ShaderTutorials/blob/master/Assets/010_Triplanar_Mapping/triplanar_mapping.shader
希望你能喜欢这个教程哦!如果你想支持我,可以关注我的推特,或者通过ko-fi、或patreon给两小钱。总之,各位大爷,走过路过不要错过,有钱的捧个钱场,没钱的捧个人场:-)!!!







