原文:
Perlin Noise
Perlin Noise
泊林噪声也是非常常用的一种噪声。和上一篇值类噪声非常相似,泊林噪声也是基于噪声色块,是“梯度噪声”实现方式的一种,所以容易产生重复、光滑的效果。它们之间的区别在于本篇将上上一篇得到的噪声当做方向来处理,而值类噪声则将其当做值来处理。因为噪声部分内容复杂,建议你先从噪点、和值类噪声开始学习。

Gradient Noise in one Dimension
泊林噪声是多维梯度噪声中的一种。因为一维梯度噪声比较简单,所以我们先从它入手。
首先我们实现一维噪声生成着色器,并且把所有相关代码封装到noise函数中,方便阅读。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| float gradientNoise(float value){
float previousCellNoise = rand1dTo1d(floor(value));
float nextCellNoise = rand1dTo1d(ceil(value));
float interpolator = frac(value);
interpolator = easeInOut(interpolator);
return lerp(previousCellNoise, nextCellNoise, interpolator);
}
void surf (Input i, inout SurfaceOutputStandard o) {
float value = i.worldPos.x / _CellSize;
float noise = perlinNoise(value);
float dist = abs(noise - i.worldPos.y);
float pixelHeight = fwidth(i.worldPos.y);
float lineIntensity = smoothstep(2*pixelHeight, pixelHeight, dist);
o.Albedo = lerp(1, 0, lineIntensity);
}
|
正如开篇提到的,泊林噪声是将初始的随机噪声当做方向来处理,然后在此基础上进行进一步平滑操作。因此我们首先要计算梯度。梯度方向可上可下,因此我们需要将噪声值从[0,1]区间变换到[-1,1]区间。
在前面值类噪声处理中,我们很容易得到每个色块的噪声值,但是现在我们记录的并不是色块的噪声值,而是该色块噪声变化的一种趋势,也就是前面说的方向,梯度方向。但是在平滑处理的插值运算中,我们仍然需要知道色块具体位置的噪声值,所以我们要根据这个梯度方向来重新构造一个噪声分布曲线。因为梯度的存在,这里构造的是倾斜的一段一段的直线。在前面的值类噪声中的线段是水平的,这也是值类和方向类噪声处理的实际差别。
1
2
3
4
5
6
7
8
| float gradientNoise(float value){
float fraction = frac(value);
float previousCellInclination = rand1dTo1d(floor(value)) * 2 - 1;
float previousCellLinePoint = previousCellInclination * fraction;
return previousCellLinePoint;
}
|
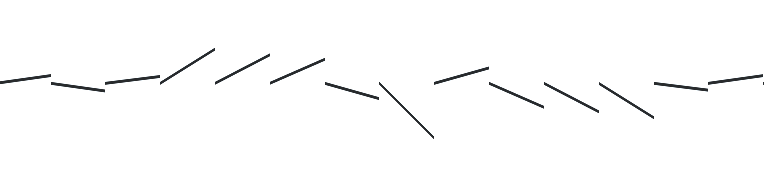
上面的线段都是沿着色块中心点沿着一个方向伸展的,色块之间没有重叠区域,所以需要去下一个色块,沿着反方向延伸。这样,两个相邻色块之间有了重叠区域,可以做插值平滑处理。而正反方向的延伸要保持在同一条直线上。因为前面定义正向延伸的区间是0到1,所以反向延伸的区间就是-1到0。
1
2
| float nextCellInclination = rand1dTo1d(ceil(value)) * 2 - 1;
float nextCellLinePoint = nextCellInclination * (fraction - 1);
|
接下来是前后两端的插值,为了保证线条连续,我们设定距离哪个色块越近,其插值权重越大。为了保证线条光滑,我们仍然使用缓动函数来平滑。
1
2
3
4
5
6
7
8
9
10
11
12
| float gradientNoise(float value){
float fraction = frac(value);
float interpolator = easeInOut(fraction);
float previousCellInclination = rand1dTo1d(floor(value)) * 2 - 1;
float previousCellLinePoint = previousCellInclination * fraction;
float nextCellInclination = rand1dTo1d(ceil(value)) * 2 - 1;
float nextCellLinePoint = nextCellInclination * (fraction - 1);
return lerp(previousCellLinePoint, nextCellLinePoint, interpolator);
}
|
另一个小改动是,在调用一维随机数函数时,我将其中不再使用乘积方式,而是改成加一个常数,这样当输入为0的时候,结果也不会永远是零。这个我在随机数那一篇文章应该也仅仅做了修改。
1
2
3
4
| float rand1dTo1d(float3 value, float mutator = 0.546){
float random = frac(sin(value + mutator) * 143758.5453);
return random;
}
|

2d Perlin Noise
对于多维泊林噪声,处理起来就比较麻烦了。首先我们噪声的需要在多个维度进行插值,并且我们的噪声梯度方向也是多维的。
1
2
3
| float perlinNoise(float2 value){
}
|
而且相邻点也有两个变为四个,也就是需要在色块的四个角点上进行噪声值采样,将采样值转换为方向向量。
1
2
3
4
| float2 lowerLeftDirection = rand2dTo2d(float2(floor(value.x), floor(value.y))) * 2 - 1;
float2 lowerRightDirection = rand2dTo2d(float2(ceil(value.x), floor(value.y))) * 2 - 1;
float2 upperLeftDirection = rand2dTo2d(float2(floor(value.x), ceil(value.y))) * 2 - 1;
float2 upperRightDirection = rand2dTo2d(float2(ceil(value.x), ceil(value.y))) * 2 - 1;
|
得到四个角点的梯度向量后,计算四个角点在当前点的贡献值。
1
2
3
4
5
6
| float2 fraction = frac(value);
float lowerLeftFunctionValue = dot(lowerLeftDirection, fraction - float2(0, 0));
float lowerRightFunctionValue = dot(lowerRightDirection, fraction - float2(0, 1));
float upperLeftFunctionValue = dot(upperLeftDirection, fraction - float2(1, 0));
float upperRightFunctionValue = dot(upperRightDirection, fraction - float2(1, 1));
|
然后对他们进行二次插值。
1
2
3
4
5
6
7
8
| float interpolatorX = easeInOut(fraction.x);
float interpolatorY = easeInOut(fraction.y);
float lowerCells = lerp(lowerLeftFunctionValue, lowerRightFunctionValue, interpolatorX);
float upperCells = lerp(upperLeftFunctionValue, upperRightFunctionValue, interpolatorX);
float noise = lerp(lowerCells, upperCells, interpolatorY);
return noise;
|
现在我们可以在片段函数中使用我们的泊林噪声函数了,因为生成的泊林噪声值是在-0.5到0.5之间,所以我们需要将其映射到0到1之间。
1
2
3
4
5
6
| void surf (Input i, inout SurfaceOutputStandard o) {
float2 value = i.worldPos.xz / _CellSize;
float noise = perlinNoise(value) + 0.5;
o.Albedo = noise;
}
|

3d Perlin Noise
三维泊林噪声和上一遍的值类噪声很类似,只不过在最内层循环中,我们不能直接得到噪声值,而是需要通过梯度方向来计算噪声值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| float perlinNoise(float3 value){
float3 fraction = frac(value);
float interpolatorX = easeInOut(fraction.x);
float interpolatorY = easeInOut(fraction.y);
float interpolatorZ = easeInOut(fraction.z);
float cellNoiseZ[2];
[unroll]
for(int z=0;z<=1;z++){
float cellNoiseY[2];
[unroll]
for(int y=0;y<=1;y++){
float cellNoiseX[2];
[unroll]
for(int x=0;x<=1;x++){
float3 cell = floor(value) + float3(x, y, z);
float3 cellDirection = rand3dTo3d(cell) * 2 - 1;
float3 compareVector = fraction - float3(x, y, z);
cellNoiseX[x] = dot(cellDirection, compareVector);
}
cellNoiseY[y] = lerp(cellNoiseX[0], cellNoiseX[1], interpolatorX);
}
cellNoiseZ[z] = lerp(cellNoiseY[0], cellNoiseY[1], interpolatorY);
}
float noise = lerp(cellNoiseZ[0], cellNoiseZ[1], interpolatorZ);
return noise;
}
|
然后在片段着色器中,我们使用三维向量就可以生成三维泊林噪声了。
1
2
3
4
5
6
7
| void surf (Input i, inout SurfaceOutputStandard o) {
float3 value = i.worldPos / _CellSize;
float noise = perlinNoise(value) + 0.5;
o.Albedo = noise;
}
|
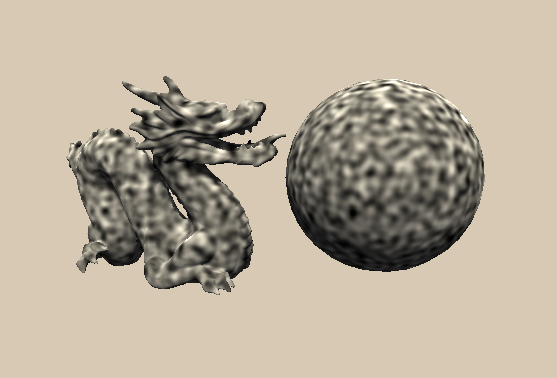
Special Use Case
泊林噪声看起来像行为怪异的云朵,但是可以实现一些有趣的效果。
首先,我们可以将相同值的泊林噪声点相连接,形成类似地图等高线的图案。首先我们将噪声值放大,然后取其小数部分。
1
2
3
4
5
6
7
| float3 value = i.worldPos / _CellSize;
float noise = perlinNoise(value) + 0.5;
noise = frac(noise * 6);
o.Albedo = noise;
|

然后我们来实现光滑的等高线。首先我们需要计算一个像素内的噪声变化情况,这里我们可以使用fwidth函数。然后使用smoothstep函数来剔除小于1的像素,因为像素是离散分布的,所以有些像素只能近似等于1,所以需要以一个像素内的变化值来做近似处理。同样的我们再剔除大于0的像素,两次剔除得到的边界相叠加。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void surf (Input i, inout SurfaceOutputStandard o) {
float3 value = i.worldPos / _CellSize;
float noise = perlinNoise(value) + 0.5;
noise = frac(noise * 6);
float pixelNoiseChange = fwidth(noise);
float heightLine = smoothstep(1-pixelNoiseChange, 1, noise);
heightLine += smoothstep(pixelNoiseChange, 0, noise);
o.Albedo = heightLine;
}
|

还有一个使用多维噪声的技巧,就是将其中一个不用的维度抽出来,加上时间变量,这样随着时间的改变,我们的噪声图也会随着变化。
1
2
3
4
| Properties {
_CellSize ("Cell Size", Range(0, 1)) = 1
_ScrollSpeed ("Scroll Speed", Range(0, 1)) = 1
}
|
1
2
3
|
float _CellSize;
float _ScrollSpeed;
|
1
2
3
4
| float3 value = i.worldPos / _CellSize;
value.y += _Time.y * _ScrollSpeed;
float noise = perlinNoise(value) + 0.5;
|

Source
1d gradient noise
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| Shader "Tutorial/026_perlin_noise/1d" {
Properties {
_CellSize ("Cell Size", Range(0, 1)) = 1
}
SubShader {
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
CGPROGRAM
#pragma surface surf Standard fullforwardshadows
#pragma target 3.0
#include "Random.cginc"
float _CellSize;
struct Input {
float3 worldPos;
};
float easeIn(float interpolator){
return interpolator * interpolator * interpolator * interpolator * interpolator;
}
float easeOut(float interpolator){
return 1 - easeIn(1 - interpolator);
}
float easeInOut(float interpolator){
float easeInValue = easeIn(interpolator);
float easeOutValue = easeOut(interpolator);
return lerp(easeInValue, easeOutValue, interpolator);
}
float gradientNoise(float value){
float fraction = frac(value);
float interpolator = easeInOut(fraction);
float previousCellInclination = rand1dTo1d(floor(value)) * 2 - 1;
float previousCellLinePoint = previousCellInclination * fraction;
float nextCellInclination = rand1dTo1d(ceil(value)) * 2 - 1;
float nextCellLinePoint = nextCellInclination * (fraction - 1);
return lerp(previousCellLinePoint, nextCellLinePoint, interpolator);
}
void surf (Input i, inout SurfaceOutputStandard o) {
float value = i.worldPos.x / _CellSize;
float noise = gradientNoise(value);
float dist = abs(noise - i.worldPos.y);
float pixelHeight = fwidth(i.worldPos.y);
float lineIntensity = smoothstep(2*pixelHeight, pixelHeight, dist);
o.Albedo = lerp(1, 0, lineIntensity);
}
ENDCG
}
FallBack "Standard"
}
|
2d perlin noise
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| Shader "Tutorial/026_perlin_noise/2d" {
Properties {
_CellSize ("Cell Size", Range(0, 1)) = 1
}
SubShader {
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
CGPROGRAM
#pragma surface surf Standard fullforwardshadows
#pragma target 3.0
#include "Random.cginc"
float _CellSize;
float _Jitter;
struct Input {
float3 worldPos;
};
float easeIn(float interpolator){
return interpolator * interpolator;
}
float easeOut(float interpolator){
return 1 - easeIn(1 - interpolator);
}
float easeInOut(float interpolator){
float easeInValue = easeIn(interpolator);
float easeOutValue = easeOut(interpolator);
return lerp(easeInValue, easeOutValue, interpolator);
}
float perlinNoise(float2 value){
float2 lowerLeftDirection = rand2dTo2d(float2(floor(value.x), floor(value.y))) * 2 - 1;
float2 lowerRightDirection = rand2dTo2d(float2(ceil(value.x), floor(value.y))) * 2 - 1;
float2 upperLeftDirection = rand2dTo2d(float2(floor(value.x), ceil(value.y))) * 2 - 1;
float2 upperRightDirection = rand2dTo2d(float2(ceil(value.x), ceil(value.y))) * 2 - 1;
float2 fraction = frac(value);
float lowerLeftFunctionValue = dot(lowerLeftDirection, fraction - float2(0, 0));
float lowerRightFunctionValue = dot(lowerRightDirection, fraction - float2(1, 0));
float upperLeftFunctionValue = dot(upperLeftDirection, fraction - float2(0, 1));
float upperRightFunctionValue = dot(upperRightDirection, fraction - float2(1, 1));
float interpolatorX = easeInOut(fraction.x);
float interpolatorY = easeInOut(fraction.y);
float lowerCells = lerp(lowerLeftFunctionValue, lowerRightFunctionValue, interpolatorX);
float upperCells = lerp(upperLeftFunctionValue, upperRightFunctionValue, interpolatorX);
float noise = lerp(lowerCells, upperCells, interpolatorY);
return noise;
}
void surf (Input i, inout SurfaceOutputStandard o) {
float2 value = i.worldPos.xz / _CellSize;
float noise = perlinNoise(value) + 0.5;
o.Albedo = noise;
}
ENDCG
}
FallBack "Standard"
}
|
3d perlin noise
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| Shader "Tutorial/026_perlin_noise/3d" {
Properties {
_CellSize ("Cell Size", Range(0, 1)) = 1
}
SubShader {
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
CGPROGRAM
#pragma surface surf Standard fullforwardshadows
#pragma target 3.0
#include "Random.cginc"
float _CellSize;
float _Jitter;
struct Input {
float3 worldPos;
};
float easeIn(float interpolator){
return interpolator * interpolator;
}
float easeOut(float interpolator){
return 1 - easeIn(1 - interpolator);
}
float easeInOut(float interpolator){
float easeInValue = easeIn(interpolator);
float easeOutValue = easeOut(interpolator);
return lerp(easeInValue, easeOutValue, interpolator);
}
float perlinNoise(float3 value){
float3 fraction = frac(value);
float interpolatorX = easeInOut(fraction.x);
float interpolatorY = easeInOut(fraction.y);
float interpolatorZ = easeInOut(fraction.z);
float cellNoiseZ[2];
[unroll]
for(int z=0;z<=1;z++){
float cellNoiseY[2];
[unroll]
for(int y=0;y<=1;y++){
float cellNoiseX[2];
[unroll]
for(int x=0;x<=1;x++){
float3 cell = floor(value) + float3(x, y, z);
float3 cellDirection = rand3dTo3d(cell) * 2 - 1;
float3 compareVector = fraction - float3(x, y, z);
cellNoiseX[x] = dot(cellDirection, compareVector);
}
cellNoiseY[y] = lerp(cellNoiseX[0], cellNoiseX[1], interpolatorX);
}
cellNoiseZ[z] = lerp(cellNoiseY[0], cellNoiseY[1], interpolatorY);
}
float noise = lerp(cellNoiseZ[0], cellNoiseZ[1], interpolatorZ);
return noise;
}
void surf (Input i, inout SurfaceOutputStandard o) {
float3 value = i.worldPos / _CellSize;
float noise = perlinNoise(value) + 0.5;
o.Albedo = noise;
}
ENDCG
}
FallBack "Standard"
}
|
special use tircks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| Shader "Tutorial/026_perlin_noise/special" {
Properties {
_CellSize ("Cell Size", Range(0, 1)) = 1
_ScrollSpeed ("Scroll Speed", Range(0, 1)) = 1
}
SubShader {
Tags{ "RenderType"="Opaque" "Queue"="Geometry"}
CGPROGRAM
#pragma surface surf Standard fullforwardshadows
#pragma target 3.0
#include "Random.cginc"
float _CellSize;
float _ScrollSpeed;
struct Input {
float3 worldPos;
};
float easeIn(float interpolator){
return interpolator * interpolator;
}
float easeOut(float interpolator){
return 1 - easeIn(1 - interpolator);
}
float easeInOut(float interpolator){
float easeInValue = easeIn(interpolator);
float easeOutValue = easeOut(interpolator);
return lerp(easeInValue, easeOutValue, interpolator);
}
float perlinNoise(float3 value){
float3 fraction = frac(value);
float interpolatorX = easeInOut(fraction.x);
float interpolatorY = easeInOut(fraction.y);
float interpolatorZ = easeInOut(fraction.z);
float cellNoiseZ[2];
[unroll]
for(int z=0;z<=1;z++){
float cellNoiseY[2];
[unroll]
for(int y=0;y<=1;y++){
float cellNoiseX[2];
[unroll]
for(int x=0;x<=1;x++){
float3 cell = floor(value) + float3(x, y, z);
float3 cellDirection = rand3dTo3d(cell) * 2 - 1;
float3 compareVector = fraction - float3(x, y, z);
cellNoiseX[x] = dot(cellDirection, compareVector);
}
cellNoiseY[y] = lerp(cellNoiseX[0], cellNoiseX[1], interpolatorX);
}
cellNoiseZ[z] = lerp(cellNoiseY[0], cellNoiseY[1], interpolatorY);
}
float noise = lerp(cellNoiseZ[0], cellNoiseZ[1], interpolatorZ);
return noise;
}
void surf (Input i, inout SurfaceOutputStandard o) {
float3 value = i.worldPos / _CellSize;
value.y += _Time.y * _ScrollSpeed;
float noise = perlinNoise(value) + 0.5;
noise = frac(noise * 6);
float pixelNoiseChange = fwidth(noise);
float heightLine = smoothstep(1-pixelNoiseChange, 1, noise);
heightLine += smoothstep(pixelNoiseChange, 0, noise);
o.Albedo = heightLine;
}
ENDCG
}
FallBack "Standard"
}
|
我花了很长时间来理解泊林噪声的工作原理,这里做了一些总结,希望能对你理解泊林噪声有所帮助。
你可以在以下链接找到源码:
希望你能喜欢这个教程哦!如果你想支持我,可以关注我的推特,或者通过ko-fi、或patreon给两小钱。总之,各位大爷,走过路过不要错过,有钱的捧个钱场,没钱的捧个人场:-)!!!







